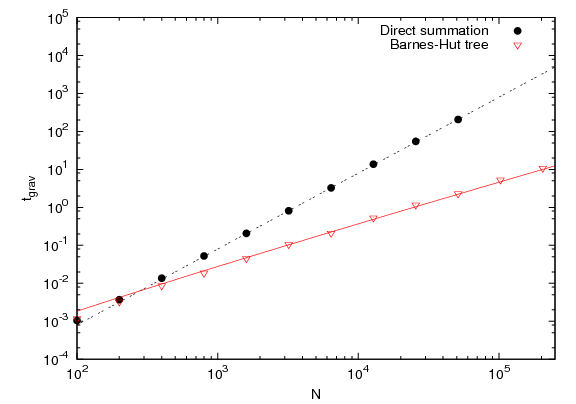
Tree scaling test
A Barnes-Hut gravity tree is expected to scale as O(N log N) where N is the total number of SPH particles compared to O(N*N) for direct-sum gravity. Here, we run a short simulation of the collapse of a uniform-density sphere using both direct-sum gravity and the Barnes-Hut gravity tree for a large range of particle numbers.
We demonstrate in the graph below that both the direct-sum
gravity and the tree follow the expected scaling laws for a wide
range in values of N (< 20,000), except at
low N where deviation is expected due to other overheads in SEREN
and low-resolution of the timing routines. We can also see that
the tree becomes more efficient than direct-sum at a relatively
low particle number (~500) which is lower than the often-quoted
number of several thousand. This is probably due to the direct-sum
terms requiring more computational clock-cycles due to the need to
include kernel-softening terms in the particle-particle calculation.